Creating a new DDM fitting function#
Here, we are going to go over how one would add a new fitting function. The function we will add is one which models a polydisperse collection of objects. We will be fitting the DDM matrix to the function:
So we will have four fitting parameters: \(A\), \(\tau\), \(\mu\), and \(B\). The relative polydispersity is given by \(\mu \tau^2\).
Importing the necessary modules#
[1]:
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np #numerical python used for working with arrays, mathematical operations
import xarray as xr #package for labeling and adding metadata to multi-dimensional arrays
import sys
sys.path.append("../../PyDDM") #must point to the PyDDM folder
import ddm_analysis_and_fitting as ddm
import ISF_and_DDMmatrix_theoretical_models as models
Creating the function#
We will first create the function for this new model in the file ISF_and_DDMmatrix_theoretical_models.py.
The first argument of this function will be the lagtime. The other arguments will be the four parameters in the model.
[2]:
####################################################################################
# THIS FUNCTION TO BE PLACED IN THE FILE `ISF_and_DDMmatrix_theoretical_models.py` #
####################################################################################
def dTheoryPolydisperse_DDM(lagtime,amplitude,tau,mu,bg):
r"""Theoretical model for the DDM matrix to account for polydisperisty
Parameters
----------
lagtime : array
1D array of the lagtimes
amplitude : float
Amplitude, "A" in equation below
tau : float
The characteristic decay time
mu : float
To account for polydispersity
bg : float
Background term, "B" in equation below
Returns
-------
ddm_matrix : array
DDM matrix as shown in equation below
Notes
-----
This model is used when polydispersity is present.
.. math::
D(q,\Delta t) = A(q) \left[ 1 - \exp \left( -\frac{\Delta t}{\tau(q)} \right) \left( 1 + \frac{\mu \tau^2}{2} \right) \right] + B(q)
"""
relative_polydisp = mu * tau * tau
isf = np.exp(-1 * (lagtime / tau)) * (1 + (relative_polydisp/2.0))
ddm_matrix = amplitude * (1 - isf) + bg
return ddm_matrix
Creating the parameters dictionary#
Next, we will create a dictionary in the file fit_parameters_dictionaries.py.
[3]:
ddm_matrix_polydisperse = {}
ddm_matrix_polydisperse['parameter_info'] = [
{'n': 0, 'value': 0, 'limits': [0,0], 'limited': [True,True],
'fixed': False, 'parname': "Amplitude", 'error': 0, 'step':0},
{'n': 1, 'value': 0, 'limits': [0,0], 'limited': [True,True],
'fixed': False, 'parname': "Tau", 'error': 0, 'step':0},
{'n': 2, 'value': 0, 'limits': [0,0], 'limited': [True,True],
'fixed': False, 'parname': "Mu", 'error': 0, 'step':0},
{'n': 3, 'value': 0, 'limits': [0,0], 'limited': [True,True],
'fixed': False, 'parname': "Background", 'error': 0, 'step':0}]
ddm_matrix_polydisperse['model_function'] = models.dTheoryPolydisperse_DDM
ddm_matrix_polydisperse['data_to_use'] = 'DDM Matrix'
Going over this dictionary
We first make an empty dictionary (we call it whatever we want):
ddm_matrix_polydisperse = {}
We then create a list of dictionaries using the key
parameter_info. The number of elements in this list should be equal to the number of fitting parameters. For this new model we are implementing, we have \(A\), \(\tau\), \(\mu\), and \(B\). Each element in this list looks something like this:
{'n': 0, 'value': 0, 'limits': [0,0], 'limited': [True,True],
'fixed': False, 'parname': "Amplitude", 'error': 0, 'step':0}
Make sure to enter in the parameter name in for the key parname. Here, we have parameter names of Amplitude, Tau, Mu, and Background. Also, the order of the paramters in parameter_info should match the order in which the arguments to the function dTheoryPolydisperse_DDM appear.
We then provide the function which we made and placed in the file
ISF_and_DDMmatrix_theoretical_models.pyin the previous step:
ddm_matrix_polydisperse['model_function'] = models.dTheoryPolydisperse_DDM
Finally, we specify whether the data to be fit is the DDM matrix or the ISF:
ddm_matrix_polydisperse['data_to_use'] = 'DDM Matrix'
Adding dictionary to the fitting models#
We next must add this dictionary that we created (ddm_matrix_polydisperse) to the dictionary fitting_models in the file fit_parameters_dictionaries.py.
Note that the key used for the dictionary fitting_models will be how we will refer to the model in the YAML file. Here, we are choosing to use the key ‘DDM Matrix - Polydisperse’.
[4]:
fitting_models = {}
fitting_models['DDM Matrix - Polydisperse'] = ddm_matrix_polydisperse
Trying out the new model!#
[13]:
import yaml
ddm_analysis_parameters_str = """
DataDirectory: 'C:/Users/rmcgorty/Documents/GitHub/DDM-at-USD/ExampleData/'
FileName: 'images_nobin_40x_128x128_8bit.tif'
Metadata:
pixel_size: 0.242 # size of pixel in um
frame_rate: 41.7 #frames per second
Analysis_parameters:
number_lag_times: 40
last_lag_time: 600
binning: no
overlap_method: 1
Fitting_parameters:
model: 'DDM Matrix - Polydisperse'
Tau: [1.0, 0.001, 10]
Mu: [0.4, 0.001, 100]
StretchingExp: [1.0, 0.5, 1.1]
Amplitude: [1e2, 1, 1e6]
Background: [2.5e4, 0, 1e7]
Good_q_range: [5, 20]
Auto_update_good_q_range: True
"""
parameters_as_dictionary = yaml.safe_load(ddm_analysis_parameters_str)
[8]:
ddm_calc = ddm.DDM_Analysis(parameters_as_dictionary)
Provided metadata: {'pixel_size': 0.242, 'frame_rate': 41.7}
Image shape: 3000-by-128-by-128
Number of frames to use for analysis: 3000
Maximum lag time (in frames): 600
Number of lag times to compute DDM matrix: 40
Using the full frame, dimensions: 128-by-128.
[9]:
ddm_calc.calculate_DDM_matrix()
The file C:/Users/rmcgorty/Documents/GitHub/DDM-at-USD/ExampleData/images_nobin_40x_128x128_8bit_ddmmatrix.nc already exists. So perhaps the DDM matrix was calculated already?
Do you still want to calculate the DDM matrix? (y/n): y
2022-02-15 11:44:34,640 - DDM Calculations - Running dt = 1...
2022-02-15 11:44:41,652 - DDM Calculations - Running dt = 5...
2022-02-15 11:44:45,105 - DDM Calculations - Running dt = 9...
2022-02-15 11:44:48,323 - DDM Calculations - Running dt = 16...
2022-02-15 11:44:52,230 - DDM Calculations - Running dt = 27...
2022-02-15 11:44:55,881 - DDM Calculations - Running dt = 47...
2022-02-15 11:44:59,466 - DDM Calculations - Running dt = 81...
2022-02-15 11:45:04,809 - DDM Calculations - Running dt = 138...
2022-02-15 11:45:07,986 - DDM Calculations - Running dt = 236...
2022-02-15 11:45:11,031 - DDM Calculations - Running dt = 402...
DDM matrix took 39.641406536102295 seconds to compute.
Background estimate ± std is 211.17 ± 1.49
[9]:
<xarray.Dataset>
Dimensions: (lagtime: 40, q_y: 128, q_x: 128, q: 64, y: 128, x: 128, frames: 40)
Coordinates:
* lagtime (lagtime) float64 0.02398 0.04796 0.07194 ... 12.59 14.36
framelag (frames) int32 1 2 3 4 5 6 7 ... 308 352 402 459 525 599
* q_y (q_y) float64 -12.98 -12.78 -12.58 ... 12.37 12.58 12.78
* q_x (q_x) float64 -12.98 -12.78 -12.58 ... 12.37 12.58 12.78
* q (q) float64 0.0 0.2028 0.4057 0.6085 ... 12.37 12.58 12.78
* y (y) int32 0 1 2 3 4 5 6 7 ... 121 122 123 124 125 126 127
* x (x) int32 0 1 2 3 4 5 6 7 ... 121 122 123 124 125 126 127
Dimensions without coordinates: frames
Data variables:
ddm_matrix_full (lagtime, q_y, q_x) float64 175.0 193.1 ... 172.1 186.3
ddm_matrix (lagtime, q) float64 0.0 295.8 314.5 ... 206.3 208.3 207.5
first_image (y, x) float64 128.0 149.0 173.0 ... 175.0 229.0 215.0
avg_image_ft (q) float64 0.0 1.293e+05 5.225e+03 ... 105.3 104.7 105.3
num_pairs_per_dt (lagtime) int32 300 300 300 300 300 ... 289 283 275 267
B float64 211.2
B_std float64 1.491
Amplitude (q) float64 -211.2 2.585e+05 1.024e+04 ... -1.699 -0.52
ISF (lagtime, q) float64 0.0 0.9997 0.9899 ... -0.6879 -6.08
Attributes: (12/16)
units: Intensity
lagtime: sec
q: μm$^{-1}$
x: pixels
y: pixels
info: ddm_matrix is the averages of FFT difference images, r...
... ...
pixel_size: 0.242
frame_rate: 41.7
number_lag_times: 40
last_lag_time: 600
binning: no
overlap_method: yes- lagtime: 40
- q_y: 128
- q_x: 128
- q: 64
- y: 128
- x: 128
- frames: 40
- lagtime(lagtime)float640.02398 0.04796 ... 12.59 14.36
array([ 0.023981, 0.047962, 0.071942, 0.095923, 0.119904, 0.143885, 0.167866, 0.191847, 0.215827, 0.263789, 0.28777 , 0.335731, 0.383693, 0.431655, 0.503597, 0.57554 , 0.647482, 0.743405, 0.863309, 0.983213, 1.127098, 1.294964, 1.486811, 1.702638, 1.942446, 2.206235, 2.541966, 2.901679, 3.309353, 3.788969, 4.316547, 4.940048, 5.659472, 6.450839, 7.386091, 8.441247, 9.640288, 11.007194, 12.589928, 14.364508]) - framelag(frames)int321 2 3 4 5 6 ... 352 402 459 525 599
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 14, 16, 18, 21, 24, 27, 31, 36, 41, 47, 54, 62, 71, 81, 92, 106, 121, 138, 158, 180, 206, 236, 269, 308, 352, 402, 459, 525, 599]) - q_y(q_y)float64-12.98 -12.78 ... 12.58 12.78
array([-12.981788, -12.778947, -12.576107, -12.373267, -12.170426, -11.967586, -11.764745, -11.561905, -11.359064, -11.156224, -10.953383, -10.750543, -10.547703, -10.344862, -10.142022, -9.939181, -9.736341, -9.5335 , -9.33066 , -9.12782 , -8.924979, -8.722139, -8.519298, -8.316458, -8.113617, -7.910777, -7.707937, -7.505096, -7.302256, -7.099415, -6.896575, -6.693734, -6.490894, -6.288053, -6.085213, -5.882373, -5.679532, -5.476692, -5.273851, -5.071011, -4.86817 , -4.66533 , -4.46249 , -4.259649, -4.056809, -3.853968, -3.651128, -3.448287, -3.245447, -3.042607, -2.839766, -2.636926, -2.434085, -2.231245, -2.028404, -1.825564, -1.622723, -1.419883, -1.217043, -1.014202, -0.811362, -0.608521, -0.405681, -0.20284 , 0. , 0.20284 , 0.405681, 0.608521, 0.811362, 1.014202, 1.217043, 1.419883, 1.622723, 1.825564, 2.028404, 2.231245, 2.434085, 2.636926, 2.839766, 3.042607, 3.245447, 3.448287, 3.651128, 3.853968, 4.056809, 4.259649, 4.46249 , 4.66533 , 4.86817 , 5.071011, 5.273851, 5.476692, 5.679532, 5.882373, 6.085213, 6.288053, 6.490894, 6.693734, 6.896575, 7.099415, 7.302256, 7.505096, 7.707937, 7.910777, 8.113617, 8.316458, 8.519298, 8.722139, 8.924979, 9.12782 , 9.33066 , 9.5335 , 9.736341, 9.939181, 10.142022, 10.344862, 10.547703, 10.750543, 10.953383, 11.156224, 11.359064, 11.561905, 11.764745, 11.967586, 12.170426, 12.373267, 12.576107, 12.778947]) - q_x(q_x)float64-12.98 -12.78 ... 12.58 12.78
array([-12.981788, -12.778947, -12.576107, -12.373267, -12.170426, -11.967586, -11.764745, -11.561905, -11.359064, -11.156224, -10.953383, -10.750543, -10.547703, -10.344862, -10.142022, -9.939181, -9.736341, -9.5335 , -9.33066 , -9.12782 , -8.924979, -8.722139, -8.519298, -8.316458, -8.113617, -7.910777, -7.707937, -7.505096, -7.302256, -7.099415, -6.896575, -6.693734, -6.490894, -6.288053, -6.085213, -5.882373, -5.679532, -5.476692, -5.273851, -5.071011, -4.86817 , -4.66533 , -4.46249 , -4.259649, -4.056809, -3.853968, -3.651128, -3.448287, -3.245447, -3.042607, -2.839766, -2.636926, -2.434085, -2.231245, -2.028404, -1.825564, -1.622723, -1.419883, -1.217043, -1.014202, -0.811362, -0.608521, -0.405681, -0.20284 , 0. , 0.20284 , 0.405681, 0.608521, 0.811362, 1.014202, 1.217043, 1.419883, 1.622723, 1.825564, 2.028404, 2.231245, 2.434085, 2.636926, 2.839766, 3.042607, 3.245447, 3.448287, 3.651128, 3.853968, 4.056809, 4.259649, 4.46249 , 4.66533 , 4.86817 , 5.071011, 5.273851, 5.476692, 5.679532, 5.882373, 6.085213, 6.288053, 6.490894, 6.693734, 6.896575, 7.099415, 7.302256, 7.505096, 7.707937, 7.910777, 8.113617, 8.316458, 8.519298, 8.722139, 8.924979, 9.12782 , 9.33066 , 9.5335 , 9.736341, 9.939181, 10.142022, 10.344862, 10.547703, 10.750543, 10.953383, 11.156224, 11.359064, 11.561905, 11.764745, 11.967586, 12.170426, 12.373267, 12.576107, 12.778947]) - q(q)float640.0 0.2028 0.4057 ... 12.58 12.78
array([ 0. , 0.20284 , 0.405681, 0.608521, 0.811362, 1.014202, 1.217043, 1.419883, 1.622723, 1.825564, 2.028404, 2.231245, 2.434085, 2.636926, 2.839766, 3.042607, 3.245447, 3.448287, 3.651128, 3.853968, 4.056809, 4.259649, 4.46249 , 4.66533 , 4.86817 , 5.071011, 5.273851, 5.476692, 5.679532, 5.882373, 6.085213, 6.288053, 6.490894, 6.693734, 6.896575, 7.099415, 7.302256, 7.505096, 7.707937, 7.910777, 8.113617, 8.316458, 8.519298, 8.722139, 8.924979, 9.12782 , 9.33066 , 9.5335 , 9.736341, 9.939181, 10.142022, 10.344862, 10.547703, 10.750543, 10.953383, 11.156224, 11.359064, 11.561905, 11.764745, 11.967586, 12.170426, 12.373267, 12.576107, 12.778947]) - y(y)int320 1 2 3 4 5 ... 123 124 125 126 127
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127]) - x(x)int320 1 2 3 4 5 ... 123 124 125 126 127
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127])
- ddm_matrix_full(lagtime, q_y, q_x)float64175.0 193.1 186.5 ... 172.1 186.3
array([[[174.99021037, 193.13576207, 186.50701195, ..., 180.40963877, 186.50701195, 193.13576207], [187.70411604, 194.0283026 , 190.69078549, ..., 207.18686542, 206.30656923, 186.29421267], [201.60108966, 195.37067571, 181.33558203, ..., 186.58952829, 190.18564008, 206.44305275], ..., [199.70814364, 188.89730197, 184.04374709, ..., 172.83363391, 191.65342121, 199.76285058], [201.60108966, 206.44305275, 190.18564008, ..., 201.79637466, 181.33558203, 195.37067571], [187.70411604, 186.29421267, 206.30656923, ..., 184.5784093 , 190.69078549, 194.0283026 ]], [[208.68975932, 189.14151626, 190.33933628, ..., 172.88205215, 190.33933628, 189.14151626], [188.8718995 , 193.59325553, 181.80195416, ..., 200.75331288, 199.54982372, 179.4764216 ], [196.00796029, 199.78361487, 189.06650106, ..., 184.17460129, 197.24801991, 185.47853461], ... [193.43754669, 178.27978875, 187.03803463, ..., 189.38086944, 202.50625791, 182.0141194 ], [178.96170993, 181.50515922, 198.30085332, ..., 196.91302405, 202.65971429, 209.31528122], [196.32065759, 181.23105182, 178.9521835 , ..., 178.84540929, 195.69416232, 179.39073368]], [[194.41368509, 193.0757976 , 202.47750621, ..., 171.95664199, 202.47750621, 193.0757976 ], [173.46917028, 186.33357812, 172.1160557 , ..., 202.62099597, 173.94394263, 176.18198813], [199.05926668, 206.47069359, 187.42638058, ..., 199.15302717, 197.02920097, 188.52447352], ..., [194.16153164, 181.87471596, 176.23913043, ..., 183.82191076, 195.35261818, 175.22408632], [199.05926668, 188.52447352, 197.02920097, ..., 196.0802793 , 187.42638058, 206.47069359], [173.46917028, 176.18198813, 173.94394263, ..., 191.53381031, 172.1160557 , 186.33357812]]]) - ddm_matrix(lagtime, q)float640.0 295.8 314.5 ... 208.3 207.5
array([[ 0. , 295.77692211, 314.46690418, ..., 193.39777275, 194.05638524, 192.98689786], [ 0. , 449.56096543, 493.45863924, ..., 193.96854661, 195.12693391, 194.37195751], [ 0. , 545.16039913, 616.80982216, ..., 195.54266668, 196.54572267, 195.15415911], ..., [ 0. , 3257.22275673, 5572.6907139 , ..., 207.3031848 , 208.10489974, 207.01750155], [ 0. , 3322.81754852, 5551.18913734, ..., 206.70567196, 206.94779389, 205.93961236], [ 0. , 3299.10121265, 5527.46559257, ..., 206.34737166, 208.30607795, 207.4918691 ]]) - first_image(y, x)float64128.0 149.0 173.0 ... 229.0 215.0
array([[128., 149., 173., ..., 178., 224., 255.], [164., 163., 166., ..., 182., 197., 255.], [208., 182., 175., ..., 178., 210., 255.], ..., [147., 162., 162., ..., 182., 196., 165.], [201., 214., 234., ..., 189., 174., 178.], [255., 255., 255., ..., 175., 229., 215.]]) - avg_image_ft(q)float640.0 1.293e+05 ... 104.7 105.3
array([0.00000000e+00, 1.29341509e+05, 5.22511731e+03, 5.86989569e+03, 8.50478146e+03, 9.68446541e+03, 9.99103750e+03, 1.03319622e+04, 1.00264087e+04, 1.08058729e+04, 1.16343568e+04, 1.38669622e+04, 1.68988722e+04, 1.98642184e+04, 2.11800678e+04, 2.14311022e+04, 2.06130601e+04, 1.80258072e+04, 1.42561639e+04, 1.04082328e+04, 7.27537584e+03, 4.68549415e+03, 2.88015028e+03, 1.77658315e+03, 1.06139768e+03, 6.83505113e+02, 4.97908069e+02, 4.18238638e+02, 3.38383278e+02, 2.72050227e+02, 2.35672326e+02, 2.24525405e+02, 2.03430129e+02, 1.78436880e+02, 1.65009527e+02, 1.49291391e+02, 1.41201296e+02, 1.33121051e+02, 1.29764821e+02, 1.28159612e+02, 1.24131175e+02, 1.24052104e+02, 1.21220015e+02, 1.19076951e+02, 1.17509287e+02, 1.15310101e+02, 1.15268069e+02, 1.12572652e+02, 1.11849673e+02, 1.11765243e+02, 1.10247178e+02, 1.09703002e+02, 1.08834403e+02, 1.09662333e+02, 1.08597899e+02, 1.07728419e+02, 1.07789289e+02, 1.06907057e+02, 1.07036538e+02, 1.05981891e+02, 1.05125261e+02, 1.05313067e+02, 1.04737380e+02, 1.05326832e+02]) - num_pairs_per_dt(lagtime)int32300 300 300 300 ... 289 283 275 267
array([300, 300, 300, 300, 300, 300, 300, 300, 300, 299, 299, 299, 299, 299, 298, 298, 298, 297, 297, 296, 296, 295, 294, 293, 292, 291, 290, 288, 287, 285, 282, 280, 277, 274, 300, 295, 289, 283, 275, 267]) - B()float64211.2
array(211.17365621)
- B_std()float641.491
array(1.49105881)
- Amplitude(q)float64-211.2 2.585e+05 ... -1.699 -0.52
array([-2.11173656e+02, 2.58471844e+05, 1.02390610e+04, 1.15286177e+04, 1.67983893e+04, 1.91577572e+04, 1.97709014e+04, 2.04527506e+04, 1.98416438e+04, 2.14005721e+04, 2.30575400e+04, 2.75227507e+04, 3.35865707e+04, 3.95172631e+04, 4.21489620e+04, 4.26510308e+04, 4.10149466e+04, 3.58404407e+04, 2.83011541e+04, 2.06052919e+04, 1.43395780e+04, 9.15981465e+03, 5.54912690e+03, 3.34199265e+03, 1.91162170e+03, 1.15583657e+03, 7.84642482e+02, 6.25303620e+02, 4.65592900e+02, 3.32926798e+02, 2.60170996e+02, 2.37877154e+02, 1.95686602e+02, 1.45700103e+02, 1.18845397e+02, 8.74091262e+01, 7.12289354e+01, 5.50684455e+01, 4.83559858e+01, 4.51455685e+01, 3.70886933e+01, 3.69305527e+01, 3.12663737e+01, 2.69802467e+01, 2.38449170e+01, 1.94465450e+01, 1.93624826e+01, 1.39716478e+01, 1.25256899e+01, 1.23568306e+01, 9.32069947e+00, 8.23234748e+00, 6.49514954e+00, 8.15100953e+00, 6.02214129e+00, 4.28318246e+00, 4.40492236e+00, 2.64045708e+00, 2.89942014e+00, 7.90126460e-01, -9.23134186e-01, -5.47522559e-01, -1.69889697e+00, -5.19992889e-01]) - ISF(lagtime, q)float640.0 0.9997 0.9899 ... -0.6879 -6.08
array([[ 0. , 0.99967268, 0.98991184, ..., -31.46602935, -9.07552034, -33.97501358], [ 0. , 0.9990777 , 0.97243058, ..., -30.42356296, -8.44537697, -31.31140091], [ 0. , 0.99870784, 0.96038346, ..., -27.54857627, -7.61025348, -29.80714649], ..., [ 0. , 0.98821516, 0.47636633, ..., -6.0690629 , -0.80632288, -6.99271442], [ 0. , 0.98796138, 0.47846629, ..., -7.16036559, -1.48741531, -9.06560658], [ 0. , 0.98805314, 0.48078325, ..., -7.8147684 , -0.68790592, -6.08045665]])
- units :
- Intensity
- lagtime :
- sec
- q :
- μm$^{-1}$
- x :
- pixels
- y :
- pixels
- info :
- ddm_matrix is the averages of FFT difference images, ravs are the radial averages
- BackgroundMethod :
- 0
- OverlapMethod :
- 1
- DataDirectory :
- C:/Users/rmcgorty/Documents/GitHub/DDM-at-USD/ExampleData/
- FileName :
- images_nobin_40x_128x128_8bit.tif
- pixel_size :
- 0.242
- frame_rate :
- 41.7
- number_lag_times :
- 40
- last_lag_time :
- 600
- binning :
- no
- overlap_method :
- yes


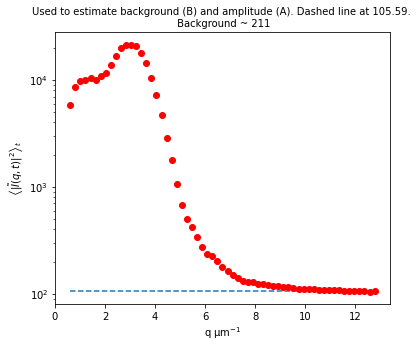
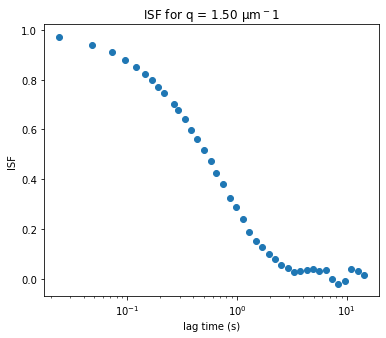
Initiazing DDM_Fit class and fitting our data to a model#
[16]:
ddm_fit = ddm.DDM_Fit(parameters_as_dictionary)
| Initial guess | Minimum | Maximum | |
|---|---|---|---|
| Amplitude | 100.0 | 1.000 | 1000000.0 |
| Tau | 1.0 | 0.001 | 10.0 |
| Mu | 0.4 | 0.001 | 100.0 |
| Background | 25000.0 | 0.000 | 10000000.0 |
Loading file C:/Users/rmcgorty/Documents/GitHub/DDM-at-USD/ExampleData/images_nobin_40x_128x128_8bit_ddmmatrix.nc ...
[17]:
fit01 = ddm_fit.fit(name_fit = 'fit01')
Fit is saved in fittings dictionary with key 'fit01'.
| q | Amplitude | Tau | Mu | Background | |
|---|---|---|---|---|---|
| 0 | 0.000000 | 1.000000 | 10.000000 | 0.003189 | 0.000000 |
| 1 | 0.202840 | 15.918614 | 4.263357 | 18.534856 | 3400.434926 |
| 2 | 0.405681 | 30.332247 | 3.518539 | 25.931651 | 5629.668970 |
| 3 | 0.608521 | 57.581148 | 2.961575 | 33.770350 | 9265.281048 |
| 4 | 0.811362 | 190.065873 | 2.145075 | 32.532448 | 14967.489051 |
| 5 | 1.014202 | 473.955467 | 1.351004 | 40.002862 | 17802.347026 |
| 6 | 1.217043 | 957.582514 | 0.975331 | 39.887403 | 18574.906136 |
| 7 | 1.419883 | 1549.598673 | 0.744532 | 42.757955 | 18671.705002 |
| 8 | 1.622723 | 2291.933349 | 0.550475 | 47.784090 | 16934.983376 |
| 9 | 1.825564 | 2975.005723 | 0.467657 | 56.028242 | 18384.154790 |
| 10 | 2.028404 | 3202.095113 | 0.404070 | 75.240054 | 20051.371018 |
| 11 | 2.231245 | 5266.187548 | 0.323464 | 81.886048 | 22482.548046 |
| 12 | 2.434085 | 7465.115533 | 0.294848 | 81.465499 | 26315.586325 |
| 13 | 2.636926 | 14184.070460 | 0.249017 | 59.968763 | 25765.143401 |
| 14 | 2.839766 | 16690.023915 | 0.220707 | 63.960972 | 25534.842535 |
| 15 | 3.042607 | 17804.609612 | 0.196756 | 74.491651 | 25061.623872 |
| 16 | 3.245447 | 17470.393043 | 0.172426 | 93.954449 | 23612.224217 |
| 17 | 3.448287 | 18728.923997 | 0.153925 | 80.094564 | 17048.030652 |
| 18 | 3.651128 | 15815.313807 | 0.137660 | 89.438046 | 12612.634732 |
| 19 | 3.853968 | 12046.238179 | 0.128386 | 94.163541 | 8782.300172 |
| 20 | 4.056809 | 8877.497642 | 0.120005 | 90.383462 | 5523.729980 |
| 21 | 4.259649 | 6030.477308 | 0.111387 | 89.458074 | 3255.010942 |
| 22 | 4.462490 | 3862.696157 | 0.103704 | 87.048636 | 1833.963963 |
| 23 | 4.665330 | 2332.250996 | 0.101411 | 91.527842 | 1167.036548 |
| 24 | 4.868170 | 1375.128511 | 0.101480 | 76.471608 | 700.101962 |
| 25 | 5.071011 | 838.960280 | 0.101001 | 69.530588 | 472.589432 |
| 26 | 5.273851 | 582.387628 | 0.099502 | 66.587505 | 379.680374 |
| 27 | 5.476692 | 463.182863 | 0.099915 | 61.930466 | 338.230561 |
| 28 | 5.679532 | 333.989714 | 0.104689 | 59.789692 | 315.095227 |
| 29 | 5.882373 | 235.423124 | 0.105729 | 68.450745 | 292.016484 |
| 30 | 6.085213 | 181.619742 | 0.115239 | 57.373480 | 279.435521 |
| 31 | 6.288053 | 181.495616 | 0.108327 | 41.251592 | 249.895779 |
| 32 | 6.490894 | 148.909799 | 0.118839 | 35.085998 | 247.667502 |
| 33 | 6.693734 | 106.653516 | 0.119293 | 46.731617 | 239.819781 |
| 34 | 6.896575 | 84.814190 | 0.136066 | 36.333522 | 233.639313 |
| 35 | 7.099415 | 62.885857 | 0.143851 | 33.363703 | 225.104853 |
| 36 | 7.302256 | 49.142341 | 0.163903 | 29.187662 | 219.586332 |
| 37 | 7.505096 | 42.414318 | 0.167708 | 25.094932 | 211.677800 |
| 38 | 7.707937 | 35.731905 | 0.186967 | 22.673872 | 213.025897 |
| 39 | 7.910777 | 34.649072 | 0.178698 | 19.759611 | 207.721937 |
| 40 | 8.113617 | 31.643594 | 0.190582 | 17.731739 | 205.457445 |
| 41 | 8.316458 | 31.576549 | 0.186011 | 17.319263 | 204.370599 |
| 42 | 8.519298 | 29.711085 | 0.189580 | 12.962045 | 201.507173 |
| 43 | 8.722139 | 25.402004 | 0.208819 | 11.838999 | 204.054317 |
| 44 | 8.924979 | 25.926379 | 0.202578 | 12.193460 | 200.751330 |
| 45 | 9.127820 | 20.655846 | 0.203674 | 15.696196 | 202.049154 |
| 46 | 9.330660 | 21.501622 | 0.200420 | 17.031168 | 201.664938 |
| 47 | 9.533500 | 18.295158 | 0.209065 | 15.326751 | 199.929263 |
| 48 | 9.736341 | 17.630038 | 0.223855 | 12.849859 | 200.833431 |
| 49 | 9.939181 | 19.752946 | 0.192329 | 14.677334 | 197.869369 |
| 50 | 10.142022 | 16.063825 | 0.209530 | 12.870744 | 199.786499 |
| 51 | 10.344862 | 15.912455 | 0.199130 | 13.444717 | 198.187176 |
| 52 | 10.547703 | 16.142997 | 0.196508 | 12.938033 | 197.286536 |
| 53 | 10.750543 | 16.155689 | 0.202991 | 9.862055 | 196.469383 |
| 54 | 10.953383 | 13.920308 | 0.225402 | 9.658823 | 197.326058 |
| 55 | 11.156224 | 13.103081 | 0.203455 | 14.857868 | 197.065425 |
| 56 | 11.359064 | 12.809598 | 0.205613 | 15.158263 | 197.532912 |
| 57 | 11.561905 | 13.027732 | 0.190986 | 15.528232 | 195.861344 |
| 58 | 11.764745 | 13.853095 | 0.218252 | 8.374395 | 196.751609 |
| 59 | 11.967586 | 14.785452 | 0.180077 | 7.701431 | 193.496723 |
| 60 | 12.170426 | 10.671071 | 0.214098 | 15.013271 | 196.189601 |
| 61 | 12.373267 | 11.071802 | 0.232047 | 13.638011 | 195.897987 |
| 62 | 12.576107 | 10.001690 | 0.251982 | 10.366264 | 196.744730 |
| 63 | 12.778947 | 11.718612 | 0.199282 | 15.029773 | 194.662109 |
Inspecting the outcome of the fit#
[18]:
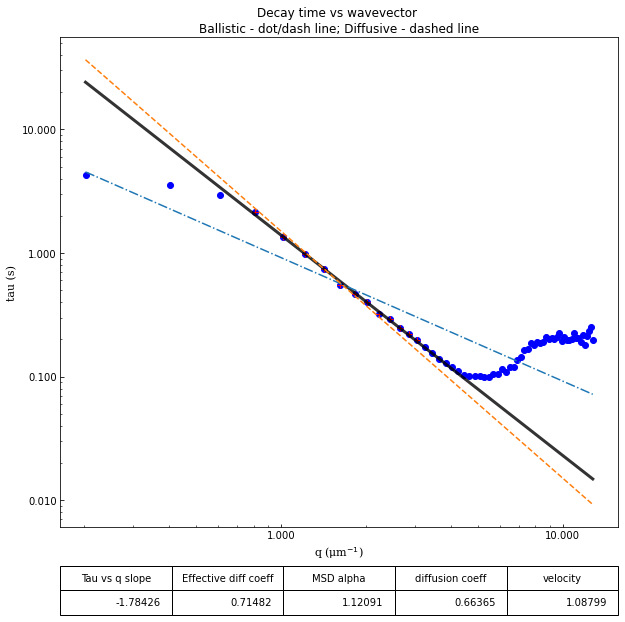
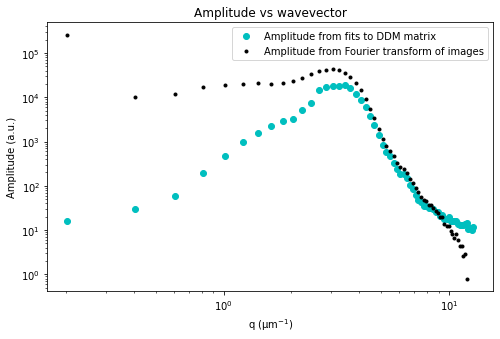
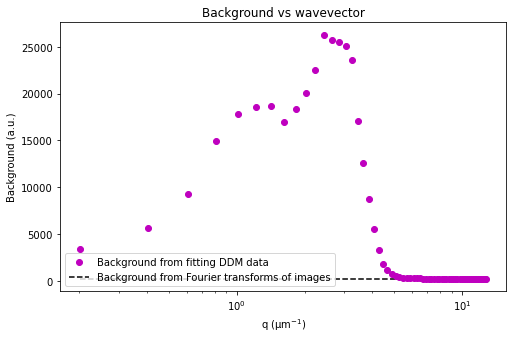
ddm.fit_report(fit01, q_indices=[3,6,9,22], forced_qs=[4,16], use_new_tau=True, show=True)
[18]:
<xarray.Dataset>
Dimensions: (parameter: 4, q: 64, lagtime: 40)
Coordinates:
* parameter (parameter) <U10 'Amplitude' 'Tau' 'Mu' 'Background'
* q (q) float64 0.0 0.2028 0.4057 0.6085 ... 12.37 12.58 12.78
* lagtime (lagtime) float64 0.02398 0.04796 0.07194 ... 12.59 14.36
Data variables:
parameters (parameter, q) float64 1.0 15.92 30.33 ... 196.7 194.7
theory (lagtime, q) float64 -0.1567 734.1 794.1 ... 206.7 206.4
isf_data (lagtime, q) float64 0.0 0.9997 0.9899 ... -0.6879 -6.08
ddm_matrix_data (lagtime, q) float64 0.0 295.8 314.5 ... 206.3 208.3 207.5
A (q) float64 -211.2 2.585e+05 1.024e+04 ... -1.699 -0.52
B float64 211.2
Attributes: (12/18)
model: DDM Matrix - Polydisperse
data_to_use: DDM Matrix
initial_params_dict: ["{'n': 0, 'value': 100.0, 'limits': [1.0...
effective_diffusion_coeff: 0.7148238989957726
tau_vs_q_slope: [-1.784258]
msd_alpha: [1.12091413]
... ...
DataDirectory: C:/Users/rmcgorty/Documents/GitHub/DDM-at...
FileName: images_nobin_40x_128x128_8bit.tif
pixel_size: 0.242
frame_rate: 41.7
BackgroundMethod: 0
OverlapMethod: 1- parameter: 4
- q: 64
- lagtime: 40
- parameter(parameter)<U10'Amplitude' 'Tau' 'Mu' 'Background'
array(['Amplitude', 'Tau', 'Mu', 'Background'], dtype='<U10')
- q(q)float640.0 0.2028 0.4057 ... 12.58 12.78
array([ 0. , 0.20284 , 0.405681, 0.608521, 0.811362, 1.014202, 1.217043, 1.419883, 1.622723, 1.825564, 2.028404, 2.231245, 2.434085, 2.636926, 2.839766, 3.042607, 3.245447, 3.448287, 3.651128, 3.853968, 4.056809, 4.259649, 4.46249 , 4.66533 , 4.86817 , 5.071011, 5.273851, 5.476692, 5.679532, 5.882373, 6.085213, 6.288053, 6.490894, 6.693734, 6.896575, 7.099415, 7.302256, 7.505096, 7.707937, 7.910777, 8.113617, 8.316458, 8.519298, 8.722139, 8.924979, 9.12782 , 9.33066 , 9.5335 , 9.736341, 9.939181, 10.142022, 10.344862, 10.547703, 10.750543, 10.953383, 11.156224, 11.359064, 11.561905, 11.764745, 11.967586, 12.170426, 12.373267, 12.576107, 12.778947]) - lagtime(lagtime)float640.02398 0.04796 ... 12.59 14.36
array([ 0.023981, 0.047962, 0.071942, 0.095923, 0.119904, 0.143885, 0.167866, 0.191847, 0.215827, 0.263789, 0.28777 , 0.335731, 0.383693, 0.431655, 0.503597, 0.57554 , 0.647482, 0.743405, 0.863309, 0.983213, 1.127098, 1.294964, 1.486811, 1.702638, 1.942446, 2.206235, 2.541966, 2.901679, 3.309353, 3.788969, 4.316547, 4.940048, 5.659472, 6.450839, 7.386091, 8.441247, 9.640288, 11.007194, 12.589928, 14.364508])
- parameters(parameter, q)float641.0 15.92 30.33 ... 196.7 194.7
array([[1.00000000e+00, 1.59186139e+01, 3.03322471e+01, 5.75811477e+01, 1.90065873e+02, 4.73955467e+02, 9.57582514e+02, 1.54959867e+03, 2.29193335e+03, 2.97500572e+03, 3.20209511e+03, 5.26618755e+03, 7.46511553e+03, 1.41840705e+04, 1.66900239e+04, 1.78046096e+04, 1.74703930e+04, 1.87289240e+04, 1.58153138e+04, 1.20462382e+04, 8.87749764e+03, 6.03047731e+03, 3.86269616e+03, 2.33225100e+03, 1.37512851e+03, 8.38960280e+02, 5.82387628e+02, 4.63182863e+02, 3.33989714e+02, 2.35423124e+02, 1.81619742e+02, 1.81495616e+02, 1.48909799e+02, 1.06653516e+02, 8.48141903e+01, 6.28858570e+01, 4.91423408e+01, 4.24143178e+01, 3.57319055e+01, 3.46490719e+01, 3.16435939e+01, 3.15765491e+01, 2.97110852e+01, 2.54020037e+01, 2.59263792e+01, 2.06558464e+01, 2.15016221e+01, 1.82951579e+01, 1.76300379e+01, 1.97529458e+01, 1.60638249e+01, 1.59124549e+01, 1.61429970e+01, 1.61556890e+01, 1.39203078e+01, 1.31030809e+01, 1.28095985e+01, 1.30277324e+01, 1.38530951e+01, 1.47854516e+01, 1.06710707e+01, 1.10718023e+01, 1.00016901e+01, 1.17186121e+01], [1.00000000e+01, 4.26335731e+00, 3.51853866e+00, 2.96157499e+00, 2.14507462e+00, 1.35100414e+00, 9.75331437e-01, 7.44532078e-01, 5.50474721e-01, 4.67657398e-01, 4.04069576e-01, 3.23463731e-01, 2.94848138e-01, 2.49017411e-01, 2.20707069e-01, 1.96755678e-01, ... 1.28498594e+01, 1.46773335e+01, 1.28707436e+01, 1.34447165e+01, 1.29380327e+01, 9.86205497e+00, 9.65882253e+00, 1.48578678e+01, 1.51582634e+01, 1.55282316e+01, 8.37439480e+00, 7.70143143e+00, 1.50132709e+01, 1.36380108e+01, 1.03662637e+01, 1.50297734e+01], [8.07119379e-24, 3.40043493e+03, 5.62966897e+03, 9.26528105e+03, 1.49674891e+04, 1.78023470e+04, 1.85749061e+04, 1.86717050e+04, 1.69349834e+04, 1.83841548e+04, 2.00513710e+04, 2.24825480e+04, 2.63155863e+04, 2.57651434e+04, 2.55348425e+04, 2.50616239e+04, 2.36122242e+04, 1.70480307e+04, 1.26126347e+04, 8.78230017e+03, 5.52372998e+03, 3.25501094e+03, 1.83396396e+03, 1.16703655e+03, 7.00101962e+02, 4.72589432e+02, 3.79680374e+02, 3.38230561e+02, 3.15095227e+02, 2.92016484e+02, 2.79435521e+02, 2.49895779e+02, 2.47667502e+02, 2.39819781e+02, 2.33639313e+02, 2.25104853e+02, 2.19586332e+02, 2.11677800e+02, 2.13025897e+02, 2.07721937e+02, 2.05457445e+02, 2.04370599e+02, 2.01507173e+02, 2.04054317e+02, 2.00751330e+02, 2.02049154e+02, 2.01664938e+02, 1.99929263e+02, 2.00833431e+02, 1.97869369e+02, 1.99786499e+02, 1.98187176e+02, 1.97286536e+02, 1.96469383e+02, 1.97326058e+02, 1.97065425e+02, 1.97532912e+02, 1.95861344e+02, 1.96751609e+02, 1.93496723e+02, 1.96189601e+02, 1.95897987e+02, 1.96744730e+02, 1.94662109e+02]]) - theory(lagtime, q)float64-0.1567 734.1 794.1 ... 206.7 206.4
array([[-1.56668585e-01, 7.34125563e+02, 7.94062470e+02, ..., 1.93318902e+02, 1.94659931e+02, 1.92889932e+02], [-1.53898122e-01, 7.49170385e+02, 8.27113813e+02, ..., 1.94659197e+02, 1.95757151e+02, 1.94419484e+02], [-1.51134296e-01, 7.64130819e+02, 8.59940659e+02, ..., 1.95867896e+02, 1.96754764e+02, 1.95775620e+02], ..., [ 6.14331613e-01, 3.21233431e+03, 5.44546299e+03, ..., 2.06969789e+02, 2.06746420e+02, 2.06380721e+02], [ 6.70787145e-01, 3.27560526e+03, 5.52318194e+03, ..., 2.06969789e+02, 2.06746420e+02, 2.06380721e+02], [ 7.24318425e-01, 3.32352697e+03, 5.57737646e+03, ..., 2.06969789e+02, 2.06746420e+02, 2.06380721e+02]]) - isf_data(lagtime, q)float640.0 0.9997 0.9899 ... -0.6879 -6.08
array([[ 0. , 0.99967268, 0.98991184, ..., -31.46602935, -9.07552034, -33.97501358], [ 0. , 0.9990777 , 0.97243058, ..., -30.42356296, -8.44537697, -31.31140091], [ 0. , 0.99870784, 0.96038346, ..., -27.54857627, -7.61025348, -29.80714649], ..., [ 0. , 0.98821516, 0.47636633, ..., -6.0690629 , -0.80632288, -6.99271442], [ 0. , 0.98796138, 0.47846629, ..., -7.16036559, -1.48741531, -9.06560658], [ 0. , 0.98805314, 0.48078325, ..., -7.8147684 , -0.68790592, -6.08045665]]) - ddm_matrix_data(lagtime, q)float640.0 295.8 314.5 ... 208.3 207.5
array([[ 0. , 295.77692211, 314.46690418, ..., 193.39777275, 194.05638524, 192.98689786], [ 0. , 449.56096543, 493.45863924, ..., 193.96854661, 195.12693391, 194.37195751], [ 0. , 545.16039913, 616.80982216, ..., 195.54266668, 196.54572267, 195.15415911], ..., [ 0. , 3257.22275673, 5572.6907139 , ..., 207.3031848 , 208.10489974, 207.01750155], [ 0. , 3322.81754852, 5551.18913734, ..., 206.70567196, 206.94779389, 205.93961236], [ 0. , 3299.10121265, 5527.46559257, ..., 206.34737166, 208.30607795, 207.4918691 ]]) - A(q)float64-211.2 2.585e+05 ... -1.699 -0.52
array([-2.11173656e+02, 2.58471844e+05, 1.02390610e+04, 1.15286177e+04, 1.67983893e+04, 1.91577572e+04, 1.97709014e+04, 2.04527506e+04, 1.98416438e+04, 2.14005721e+04, 2.30575400e+04, 2.75227507e+04, 3.35865707e+04, 3.95172631e+04, 4.21489620e+04, 4.26510308e+04, 4.10149466e+04, 3.58404407e+04, 2.83011541e+04, 2.06052919e+04, 1.43395780e+04, 9.15981465e+03, 5.54912690e+03, 3.34199265e+03, 1.91162170e+03, 1.15583657e+03, 7.84642482e+02, 6.25303620e+02, 4.65592900e+02, 3.32926798e+02, 2.60170996e+02, 2.37877154e+02, 1.95686602e+02, 1.45700103e+02, 1.18845397e+02, 8.74091262e+01, 7.12289354e+01, 5.50684455e+01, 4.83559858e+01, 4.51455685e+01, 3.70886933e+01, 3.69305527e+01, 3.12663737e+01, 2.69802467e+01, 2.38449170e+01, 1.94465450e+01, 1.93624826e+01, 1.39716478e+01, 1.25256899e+01, 1.23568306e+01, 9.32069947e+00, 8.23234748e+00, 6.49514954e+00, 8.15100953e+00, 6.02214129e+00, 4.28318246e+00, 4.40492236e+00, 2.64045708e+00, 2.89942014e+00, 7.90126460e-01, -9.23134186e-01, -5.47522559e-01, -1.69889697e+00, -5.19992889e-01]) - B()float64211.2
array(211.17365621)
- model :
- DDM Matrix - Polydisperse
- data_to_use :
- DDM Matrix
- initial_params_dict :
- ["{'n': 0, 'value': 100.0, 'limits': [1.0, 1000000.0], 'limited': [True, True], 'fixed': False, 'parname': 'Amplitude', 'error': 0, 'step': 0}", "{'n': 1, 'value': 1.0, 'limits': [0.001, 10.0], 'limited': [True, True], 'fixed': False, 'parname': 'Tau', 'error': 0, 'step': 0}", "{'n': 2, 'value': 0.4, 'limits': [0.001, 100.0], 'limited': [True, True], 'fixed': False, 'parname': 'Mu', 'error': 0, 'step': 0}", "{'n': 3, 'value': 25000.0, 'limits': [0.0, 10000000.0], 'limited': [True, True], 'fixed': False, 'parname': 'Background', 'error': 0, 'step': 0}"]
- effective_diffusion_coeff :
- 0.7148238989957726
- tau_vs_q_slope :
- [-1.784258]
- msd_alpha :
- [1.12091413]
- msd_effective_diffusion_coeff :
- [0.68638798]
- diffusion_coeff :
- 0.6636527856932951
- diffusion_coeff_std :
- 0.0915130001417818
- velocity :
- 1.087992075899325
- velocity_std :
- 0.34284091411206236
- good_q_range :
- [4, 16]
- DataDirectory :
- C:/Users/rmcgorty/Documents/GitHub/DDM-at-USD/ExampleData/
- FileName :
- images_nobin_40x_128x128_8bit.tif
- pixel_size :
- 0.242
- frame_rate :
- 41.7
- BackgroundMethod :
- 0
- OverlapMethod :
- 1
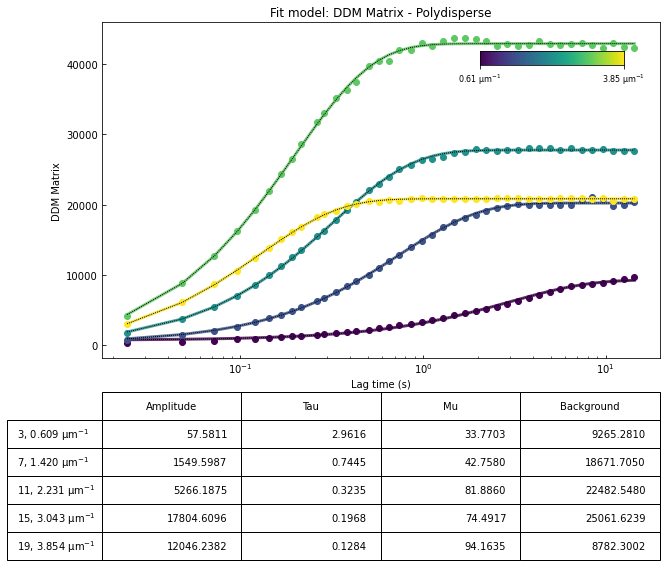
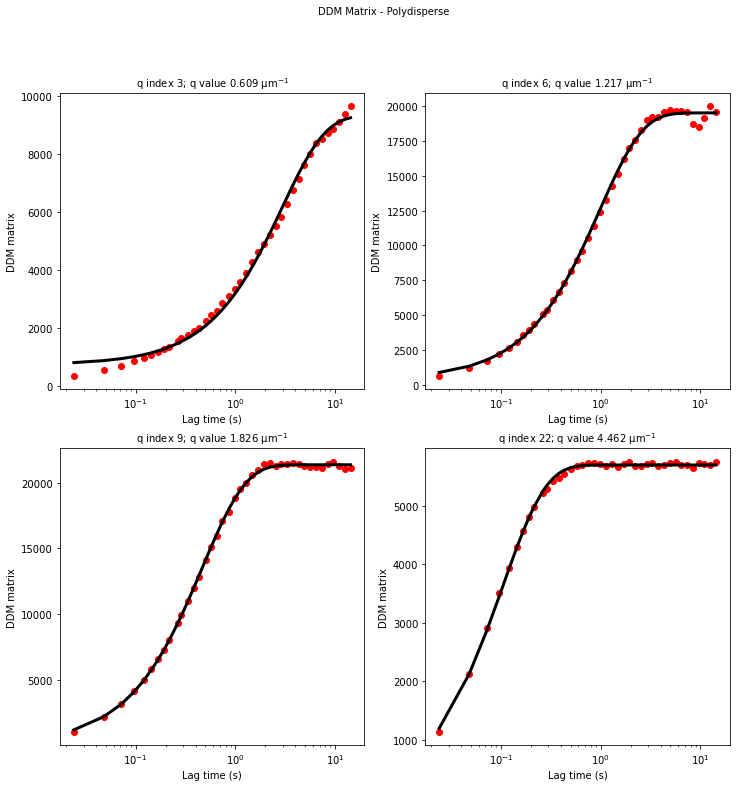
[32]:
########################################
# Plotting mu vs q #
########################################
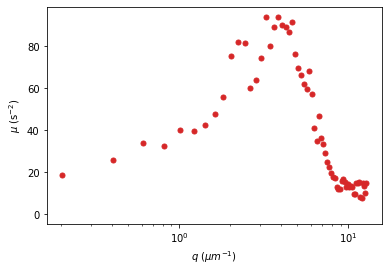
plt.figure()
plt.semilogx(fit01.q, fit01.parameters.loc['Mu'], 'o', color='tab:red', ms=5)
plt.xlabel("$q$ ($\mu m^{-1}$)")
plt.ylabel("$\mu$ (s$^{-2}$)")
########################################
# Plotting mu vs q #
########################################
plt.figure()
plt.semilogy(fit01.q, fit01.parameters.loc['Mu'] * fit01.parameters.loc['Tau']**2, 'o', color='tab:brown', ms=5)
plt.xlabel("$q$ ($\mu m^{-1}$)")
plt.ylabel("$\mu \\tau^2$")
[32]:
Text(0, 0.5, '$\\mu \\tau^2$')
[ ]: